在之前的教程中,我们研究了电阻器,它们的连接以及使用欧姆定律来计算与它们相关的电压,电流和功率。在所有情况下,电压和电流都被假定为具有恒定极性,流动和方向,换言之,直流或直流。
但是存在另一种称为交流电或交流电的电源,其电压从正到负切换,并且随着时间的推移再次返回,并且其电流相对于电压来回振荡。AC电源的振荡形状遵循“正弦波”的数学形式,其通常称为正弦波形。因此,正弦电压可被定义为V(吨)= V 最大 罪ωT。
在电感或电容值可忽略不计的交流电路中使用纯电阻时,欧姆定律的相同原理,电压,电流和功率的电路规则(甚至基尔霍夫定律)适用于直流电阻电路这一次唯一的区别是使用瞬时“峰 - 峰”或“rms”量。
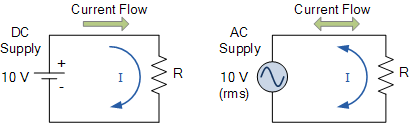
使用交流交流电压和电流时,通常只使用“rms”值以避免混淆。AC波形的均方根或“均方根”值是AC波形的有效值或DC值。用于定义AC电压源的示意性符号也是“波浪”线的示意符号,而不是DC的电池符号,如下所示。
直流和交流电源的符号表示
电阻器是“无源”器件,即它们不产生或消耗任何电能,而是将电能转换成热能。在直流电路中,电阻器中电压与电流的线性比称为其电阻。然而,在AC电路中,该电压与电流的比率取决于电源的频率和相位差或相位角( φ )。因此,使用电阻器,当在交流电路中的术语阻抗,符号Ž是通常使用的,我们可以说,直流电阻= AC阻抗,R 1 = Z。
值得注意的是,当用于交流电路时,无论从直流到非常高频的电源频率如何,电阻器总是具有相同的电阻值,这与电容器和电感器不同
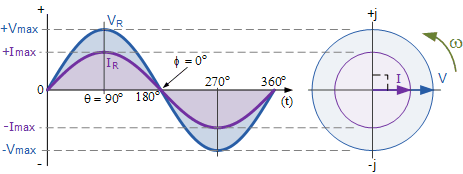
对于交流电路中的电阻器,流过它们的电流方向对电阻器的性能没有影响,因此随着电压的上升和下降而上升和下降。电流和电压达到最大值,通过零降至最小值并达到最小值。即它们同时上升和下降,据说是“同相”,如下所示。
VI相位关系和矢量图
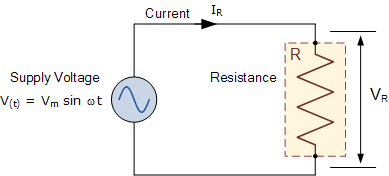
我们可以看到,在沿水平轴,该瞬时电压和电流是同相的,因为电流和电压同时达到它们的最大值的任何点,即它们的相位角 θ 是0 Ò。然后,可以比较这些电压和电流的瞬时值,以简单地通过使用欧姆定律给出电阻的欧姆值。在下面考虑由交流电源和电阻组成的电路。
电阻两端的瞬时电压V R等于电源电压V t,给出如下:
因此,在电阻器中流动的瞬时电流将是:
由于电阻两端的电压为V R = IR,因此上面电阻两端的瞬时电压也可以如下:
在纯电阻串联交流电路中,电阻上的所有电压降可以加在一起,以找到总电路电压,因为所有电压都是彼此同相的。同样,在纯电阻并联AC电路中,可以将所有单独的分支电流加在一起以找到总电路电流,因为所有分支电流彼此同相。
因为对于AC电路中的电阻器,电压和电流之间的相角φ为零,所以电路的功率因数给出为cos 0 o = 1.0。任何时刻电路中的功率都可以通过乘以该瞬间的电压和电流来找到。
然后,由电路消耗的功率(P)以P = Vrms 1cosΦ(瓦特)给出。但由于在纯电阻电路中cos(Φ)= 1,所以消耗的功率简单地给出,P = Vrms,与欧姆定律相同。
然后,这给出了“功率”波形,并且在下面显示为一系列正脉冲,因为当电压和电流都处于它们的正半周时,所得的功率为正。当电压和电流均为负时,两个负值的乘积给出正功率脉冲。
您可能需要以下产品: